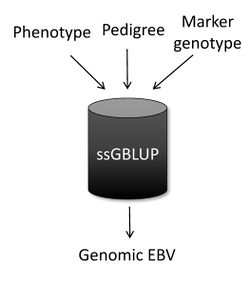
Single-step Genomic BLUP
Single-step genomic BLUP (ssGBLUP) [1][2] is a method developed to enable the inclusion of marker genotypes into the well-known BLUP methods. The idea of ssGBLUP came from the fact that only a small portion of the animals in the pedigree is genotyped. In this way, one approach to account for all animals (i.e., genotyped and non-genotyped) in the evaluation would be to combine pedigree and genomic relationships and use this as the covariance structure in the BLUP mixed-model equations. Thus, ssGBLUP uses marker information to construct genomic relationships. Legarra et al. (2009) [1] stated that genomic evaluations would be simpler if genomic relationships were available for all animals in the model. Then, their idea was to look at the pedigree relationship as a priori relationship and at the genomic relationship as the observed relationship. Based on that, they showed the genomic information could be extended (i.e., imputed) to non-genotyped animals. This means that in ssGBLUP pedigree relationships for non-genotyped animals are enhanced by the genomic information of their relatives. The relationship matrix that combines information for genotyped and non-genotyped animals is represented by H:
The subscripts 1 and 2 refer to non-genotyped and genotyped animals, respectively. A is the pedigree relationship matrix and G is the genomic relationship matrix computed based on markers. If M is a matrix of marker genotypes centered for allele frequency (p) and has the dimension of number of animals by number of single-nucleotide polymorphisms (N), G is computed as [3]:
Although H is very complicated, H-1 is quite simple [2]:
If we replace A-1 by H-1 in the BLUP mixed-model equations, we have ssGBLUP[2]:
Here b and u are vectors of fixed effects and breeding values, respectively; X and Z are incidence matrices for the effects in b and u; y is a vector of phenotypes; and λ is the ratio of residual to additive genetic variance. As a combined relationship is used in ssGBLUP, the output for each animal is automatically a genomic EBV, and the mixed-model equations above can be simplistically represented as:
The genomic EPD is then calculated as:
When the subject is genetic evaluation, one of the most common questions is “What is the main difference among ssGBLUP, BLUP, and genomic BLUP (GBLUP)?” In a nutshell, ssGBLUP uses phenotypes, pedigree, and genotypes for both genotyped and non-genotyped animals, whereas BLUP uses phenotypes and pedigree for all animals and GBLUP uses phenotypes and genotypes only for genotyped animals.
In the US, ssGBLUP has been used for genomic evaluation of beef and dairy cattle, pigs, chickens, and fish. Regarding to beef cattle, Angus Genetics Inc. runs ssGBLUP evaluations for American Angus and Charolais, Canadian Angus, Red Angus, and Charolais, and Maine Anjou. Moreover, Livestock Genetic Services (A Neogen Company) runs ssGBLUP evaluations for Santa Gertrudis. For more information about ssGBLUP for beef cattle evaluation check Lourenco et al. (2015) [4], Lourenco et al. (2017) [5], and Misztal & Lourenco (2018) [6].
ssGBLUP for large genotyped populations
Running ssGBLUP evaluations for large genotyped populations can be a huge computational challenge. This is because the construction of H-1 requires the construction and inversion of G. Matrix inversion has a cubic computational cost, requiring a large amount of memory. As an example, inverting G for 100,000 animals requires about 300Gb of memory and takes over 2 hours.
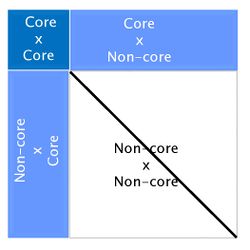
The algorithm for proven and young (APY) was proposed by Misztal et al. (2014) [7] to overcome this computing limitation of ssGBLUP, and was based on Henderson’s algorithm to construct A-1 [8]. In APY, G-1 is constructed directly, avoiding the matrix inversion step. In this algorithm, genotyped animals are split into two groups: core (c) and non-core (n). Breeding values of non-core animals are then calculated as functions of breeding values of core animals and the genomic relationships between core and non-core. If the number of genotyped animals surpasses 100,000, using APY G-1 in ssGBLUP is highly recommended. Constructing APY G-1 is computationally efficient because it requires only the inversion of a block of G that contains relationships between core animals:
Here Mnn-1 is the Mendelian error. Although this formula looks complicated, a simple graphic representation of APY G-1 is:
Looking at the above figure it is easy to see that relationships between non-core animals are ignored in APY. However, this does not have an impact on breeding values. Several studies have reported correlations greater than 0.99 between genomic EPD from regular ssGBLUP and from ssGBLUP with APY G-1 [4] [9] [10].
Genomic EPD accuracy in ssGBLUP
When data sets are very large, using the inverse of the left-hand side of the ssGBLUP mixed-model equations to calculate accuracy of genomic EPD is impeditive. Sampling techniques or approximations [11] [12] can help to overcome this limitation. The approximated genomic EPD accuracy developed by the Animal Breeding and Genetics Group at University of Georgia combines contributions from phenotypes and pedigree [13] with contribution from genomic relationships. To reduce computing time, only coefficients from the diagonal of G are used in the formula to compute genomic contribution.
Marker effects in ssGBLUP
Although the marker information in ssGBLUP is used to construct genomic relationships, it is possible to calculate SNP effects once we obtain genomic EBV (Wang et al., 2012[14], Lourenco et al., 2015[4]):
and k is the ratio of marker variance to additive genetic variance. Marker effects can be then used to calculate predictions based only on marker genotypes for young genotyped animals that are not yet or will never make into an official evaluation. This type of prediction is called direct genomic value (DGV) or molecular breeding value (MBV):
References
- ↑ 1.0 1.1 Legarra, A., I. Aguilar, and I. Misztal. 2009. A relationship matrix including full pedigree and genomic information. J. Dairy Sci. 92:4656-4663.
- ↑ 2.0 2.1 2.2 Aguilar, I., I. Misztal, D. L. Johnson, A. Legarra, S. Tsuruta, and T. J. Lawlor. 2010. Hot topic: A unified approach to utilize phenotypic, full pedigree, and genomic information for genetic evaluation of Holstein final score. Journal of Dairy Science 93: 743-752.
- ↑ VanRaden, P. M. 2008. Efficient methods to compute genomic predictions. J. Dairy Sci. 91:4414-4423.
- ↑ 4.0 4.1 4.2 Lourenco, D. A. L., S. Tsuruta, B. O. Fragomeni, Y. Masuda, I. Aguilar, A. Legarra, J. K. Bertrand, T. Amen, L. Wang, D. W. Moser, and I. Misztal. 2015. Genetic evaluation using single-step genomic best linear unbiased predictor in American Angus. Journal of Animal Science 93: 2653-2662.
- ↑ Lourenco, D.A.L., J.K. Bertrand, H.L. Bradford, S. Miller, and I. Misztal. 2017. The promise of genomics for beef improvement. BIF Meeting (http://www.bifconference.com/bif2017/proceedings/01-lourenco.pdf)
- ↑ Misztal, I. and D. Lourenco. 2018. Current research in unweighted and weighted ssGBLUP. In Proc. Beef Improvement Federation 11th genetic prediction workshop 11:6-13.
- ↑ Misztal, I., A. Legarra, and I. Aguilar. 2014. Using recursion to compute the inverse of the genomic relationship matrix. J. Dairy Sci. 97: 3943–3952.
- ↑ Henderson, C.R. 1976. A simple method for computing the inverse of a numerator relationship matrix used in the prediction of breeding values. Biometrics 32:69-83.
- ↑ Fragomeni, B. O., D. A. L. Lourenco, S. Tsuruta, Y. Masuda, I. Aguilar, A. Legarra, T. J. Lawlor, and I. Misztal. 2015. Hot topic: Use of genomic recursions in single-step genomic best linear unbiased predictor (BLUP) with a large number of genotypes. J. Dairy Sci. 98:4090-4094.
- ↑ Masuda Y., I. Misztal, S. Tsuruta, A. Legarra, I. Aguilar, D.A.L. Lourenco, B.O. Fragomeni, T.J Lawlor. 2016. Implementation of genomic recursions in single-step genomic best linear unbiased predictor for US Holsteins with a large number of genotyped animals. J. Dairy Sci. 99:1968-74.
- ↑ Tsuruta, S., D. Lourenco, Y. Masuda, D.W. Moser, and I. Misztal. 2016. Practical approximation of accuracy in genomic breeding values for a large number of genotyped animals. J. Anim. Sci. 94:162.
- ↑ Edel, C., E.C.G. Pimentel, M. Erbe, R. Emmerling, and K.U. Gotz. 2019. Short Communication: Calculating analytical reliabilities for single-step predictions. J. Dairy Sci. 102:1-7.
- ↑ Misztal, I. and Wiggans, G.R. 1988. Approximation of prediction error variance in large-scale animal models. J. Dairy Sci. 71: 27-32.
- ↑ Wang, H., I. Misztal, I. Aguilar, A. Legarra, and W. M. Muir. 2012. Genome-wide association mapping including phenotypes from relatives without genotypes. Genet. Res. 94(2):73-83.