Enhanced comment feature has been enabled for all readers including those not logged in. Click on the Discussion tab (top left) to add or reply to discussions.
Genetic Evaluation
EPD
Utility (compared to actual/adjusted phenotypes, ratios, disjoined marker scores, etc.) (Suggested writer: Megan Rolf)
Utility of Expected Progeny Differences
The estimation of breeding values, which reflect the value of an animal as a parent for the next generation, or Expected Progeny Differences (EPD), which are simply half of a breeding value, was a major advancement in the ability to select animals to fit production goals. Prior to the development of EPDs the primary method for genetic improvement was some form of subjective visual appraisal[1]. Since the development of methodology to implement Genetic Evaluation in the beef industry (launched in the 1970s)[1], EPDs have been the gold standard for genetic selection. Regardless of their associated accuracy value, they are the best selection tool that producers have to improve genetic merit in a single trait, though indices incorporate EPD information and are the best tools for multi-trait selection. Nevertheless, there is often confusion surrounding the best tools and information on which to make selection decisions. Phenotypes for quantitative traits are a combination of influences from both genetics (additive, dominance, epistatic) and the environment (permanent and temporary). Alternatively, we can write this as an equation as follows:
P=μ+G+E
where P represents phenotype, μ represents the average phenotypic value for all animals in the population, G is the genotypic value of the individual for the trait and E represents the environmental effect on the animal’s performance[2]. If we expand the equation to define genetic and environmental effects on the phenotype, we can write the equation as follows:
P=μ+A+D+I+EP+ET+GxE
where P and μ are as previously defined, A represents additive genetic effects, D represents dominance, I represents epistasis, EP represents permanent environmental effects, ET represents temporary environmental effects, and GxE represents interactions between genotype and environment[2][3].
EPDs describe the additive genetic merit of an individual and reflect its value as a parent. It is important to remember that environmental influences are not heritable, and the only genetic influence that is known to be stably inherited at this time is additive genetic variation, though dominance can be managed through crossbreeding systems. EPDs and indices are the best tools for genetic selection and do reflect average progeny performance[4][5].
The challenge with selection on measures of phenotype is that they include both genetic and environmental effects, even if weights are adjusted and/or ratios (which limit comparisons to within contemporary groups) are utilized. When selection decisions are made on these metrics, selection emphasis is also placed on nongenetic factors, which reduces the efficacy of selection and reduces genetic progress. Superiority of selection using EPDs (or breeding values) as compared to phenotypes has been demonstrated[6][7][8][9]. EPDs also simplify selection decisions. Selection using phenotypes can involve the individual’s own phenotype as well as phenotypes on relatives (including progeny, parents, and siblings, as an example). With Genetic Evaluation, all of this information is combined and weighted appropriately in a single value, the EPD, which simplifies selection. This same value is even more relevant in the genomics era, because genomic testing provides another source of information for selection. The Beef Improvement Federation recommends using genomically-enhanced EPDs, as opposed to using disjoined marker scores and EPDs separately, as the best method for utilizing genomic data for selection[10]. Genetic Evaluation methodologies are always evolving and improving, but all of these methods incorporate all available data on an animal into EPD prediction, including genomic data, and weight it appropriately so that there is a single metric for genetic selection that represents the best estimate of that animal’s genetic merit using all available data.
References: Template:Reflist
Basic Models
BLUP
Single-step Genomic BLUP
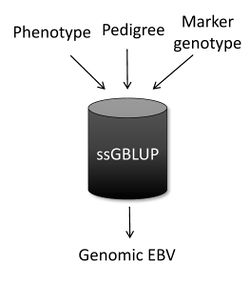
Single-step genomic BLUP (ssGBLUP) [11][12] is a method developed to enable the inclusion of marker genotypes into the well-known BLUP machinery. The idea of ssGBLUP came from the fact that only a small portion of the animals in the pedigree is genotyped. In this way, one approach to account for all animals (i.e., genotyped and non-genotyped) in the evaluation would be to combine pedigree and genomic relationships and use this as the covariance structure in the BLUP mixed model equations. Thus, ssGBLUP uses marker information to construct genomic relationships. Legarra et al. (2009) [11] stated that genomic evaluations would be simpler if genomic relationships were available for all animals in the model. Then, their idea was to look at the pedigree relationship as a priori relationship and at the genomic relationship as the observed relationship. Based on that, they showed the genomic information could be extended (i.e., imputed) to non-genotyped animals. This means that in ssGBLUP pedigree relationships for non-genotyped animals are enhanced by the genomic information of their relatives. The relationship matrix that combines information for genotyped and non-genotyped animals is represented by H:
Where the subscripts 1 and 2 refer to non-genotyped and genotyped animals, respectively. A is the pedigree relationship matrix and G is the genomic relationship matrix computed based on markers. If M is a matrix of marker genotypes centered for allele frequency (p) and has the dimension of number of animals by number of SNP (N), G is computed as [13]:
Although H is very complicated, H-1 is quite simple [12]:
If we replace A-1 by H-1 in the BLUP mixed model equations, we have ssGBLUP[12]:
Where b and u are vectors of fixed effects and breeding values, respectively; X and Z are incidence matrices for the effects in b and u; y is a vector of phenotypes, and λ is the ratio of residual to additive genetic variance. As a combined relationship is used in ssGBLUP, the output for each animal is automatically a genomic EBV, and the mixed model equations above can be simplistically represented as:
The genomic EPD is then calculated as:
When the subject is genetic evaluation, one of the most common questions is “What is the main difference among ssGBLUP, BLUP, and genomic BLUP (GBLUP)?” In a nutshell, ssGBLUP uses phenotypes, pedigree, and genotypes for both genotyped and non-genotyped animals, whereas BLUP uses phenotypes and pedigree for all animals and GBLUP uses phenotypes and genotypes only for genotyped animals.
In the US, ssGBLUP has been used for genomic evaluation of beef and dairy cattle, pigs, chickens, and fish. Regarding to beef cattle, Angus Genetics Inc. runs ssGBLUP evaluations for American Angus and Charolais, Canadian Angus, Red Angus, and Charolais, and Maine Anjou. Moreover, Livestock Genetic Services (A Neogen Company) runs ssGBLUP evaluations for Santa Gertrudis. For more information about ssGBLUP for beef cattle evaluation check Lourenco et al. (2015) [14], Lourenco et al. (2017) [15], and Misztal & Lourenco (2018) [16].
ssGBLUP for large genotyped populations
Running ssGBLUP evaluations for large genotyped populations can be a huge computational challenge. This is because the construction of H-1 requires the construction and inversion of G. Matrix inversion has a cubic computational cost, requiring a large amount of memory. As an example, inverting G for 100,000 animals requires about 300Gb of memory and takes over 2 hours.
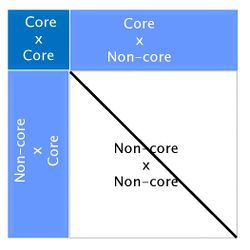
The algorithm for proven and young (APY) was proposed by Misztal et al. (2014) [17] to overcome this computing limitation of ssGBLUP, and was based on Henderson’s algorithm to construct A-1 [18]. In APY, G-1 is constructed directly, avoiding the matrix inversion step. In this algorithm, genotyped animals are split into two groups: core (c) and non-core (n). Breeding values of non-core animals are then calculated as functions of breeding values of core animals and the genomic relationships between core and non-core. If the number of genotyped animals surpasses 100,000, using APY G-1 in ssGBLUP is highly recommended. Constructing APY G-1 is computationally efficient because it requires only the inversion of a block of G that contains relationships between core animals:
Where Mnn-1 is the Mendelian error. Although this formula looks complicated, a simple graphic representation of APY G-1 is:
Looking at the above figure it is easy to see that relationships between non-core animals are ignored in APY. However, this does not have an impact on breeding values. Several studies have reported correlations greater than 0.99 between genomic EPD from regular ssGBLUP and from ssGBLUP with APY G-1 [14] [19] [20].
Genomic EPD accuracy in ssGBLUP
When datasets are very large, using the inverse of the left-hand side of the ssGBLUP mixed model equations to calculate accuracy of genomic EPD is impeditive. Sampling techniques or approximations [21] [22] can help to overcome this limitation. The approximated genomic EPD accuracy developed by the Animal Breeding and Genetics Group at University of Georgia combines contributions from phenotypes and pedigree [23] with contribution from genomic relationships. To reduce computing time, only coefficients from the diagonal of G are used in the formula to compute genomic contribution.
Marker effects in ssGBLUP
Although the marker information in ssGBLUP is used to construct genomic relationships, it is possible to calculate SNP effects once we obtain genomic EBV (Wang et al., 2012[24], Lourenco et al., 2015[14]):
Where k is the ratio of marker variance to additive genetic variance. Marker effects can be then used to calculate predictions based only on marker genotypes for young genotyped animals that are not yet or will never make into an official evaluation. This type of prediction is called direct genomic value (DGV) or molecular breeding value (MBV):
References
- ↑ 1.0 1.1 Golden, BL, DJ Garrick, and LL Benyshek. 2009. Milestones in beef cattle genetic evaluation. J Anim Sci. 87(E. Suppl.):E3-E10.
- ↑ 2.0 2.1 Bourdon, RM. 2000. Understanding Animal Breeding. Second edition. Prentice Hall, Upper Saddle River, NJ.
- ↑ Pierce, BA. 2016. Genetics Essentials. Third edition. MacMillan, New York, New York.
- ↑ Thrift, FA and TA Thrift. 2006. Review: Expected versus realized progeny differences for various beef cattle traits. Prof Anim Sci. 22:413-423.
- ↑ Kuehn, LA and RM Thallman. 2017. Across-breed EPD tables for the year 2017 adjusted to breed differences for birth year of 2015. Proceedings of the Beef Improvement Federation Annual Meeting and Research Symposium. Pages 112-144.
- ↑ Gall, GAE and Y Bakar. 2002. Application of mixed-model techniques to fish breed improvement: analysis of breeding-value selection to increase 98-day body weight in tilapia. Aquaculture. 212(1-4):93-113.
- ↑ Kuhlers, DL and BW Kennedy. 1992. Effect of culling on selection response using phenotypic selection or best linear unbiased prediction of breeding values in small, closed herds of swine. J Anim Sci. 70(8):2338-2348.
- ↑ Belonsky, GM and BW Kennedy. 1988. Selection on individual phenotype and best linear unbiased predictor of breeding values in a closed swine herd. J. Anim Sci. 66:1124-1131.
- ↑ Hagger, C. 1991. Effects of selecting on phenotype, on index, or on breeding values, on expected response, genetic relationships, and accuracy of breeding values in an experiment. J Anim Breed Genet. 108:102-110.
- ↑ Muir, WM. 2007. Comparison of genomic and traditional BLUP-estimated breeding value accuracy and selection response under alternative trait and genomic parameters. J. Anim Brdg Genet. 124(6):342-355.
- ↑ 11.0 11.1 Legarra, A., I. Aguilar, and I. Misztal. 2009. A relationship matrix including full pedigree and genomic information. J. Dairy Sci. 92:4656-4663.
- ↑ 12.0 12.1 12.2 Aguilar, I., I. Misztal, D. L. Johnson, A. Legarra, S. Tsuruta, and T. J. Lawlor. 2010. Hot topic: A unified approach to utilize phenotypic, full pedigree, and genomic information for genetic evaluation of Holstein final score. Journal of Dairy Science 93: 743-752.
- ↑ VanRaden, P. M. 2008. Efficient methods to compute genomic predictions. J. Dairy Sci. 91:4414-4423.
- ↑ 14.0 14.1 14.2 Lourenco, D. A. L., S. Tsuruta, B. O. Fragomeni, Y. Masuda, I. Aguilar, A. Legarra, J. K. Bertrand, T. Amen, L. Wang, D. W. Moser, and I. Misztal. 2015. Genetic evaluation using single-step genomic best linear unbiased predictor in American Angus. Journal of Animal Science 93: 2653-2662.
- ↑ Lourenco, D.A.L., J.K. Bertrand, H.L. Bradford, S. Miller, and I. Misztal. 2017. The promise of genomics for beef improvement. BIF Meeting (http://www.bifconference.com/bif2017/proceedings/01-lourenco.pdf)
- ↑ Misztal, I. and D. Lourenco. 2018. Current research in unweighted and weighted ssGBLUP. In Proc. Beef Improvement Federation 11th genetic prediction workshop 11:6-13.
- ↑ Misztal, I., A. Legarra, and I. Aguilar. 2014. Using recursion to compute the inverse of the genomic relationship matrix. J. Dairy Sci. 97: 3943–3952.
- ↑ Henderson, C.R. 1976. A simple method for computing the inverse of a numerator relationship matrix used in the prediction of breeding values. Biometrics 32:69-83.
- ↑ Fragomeni, B. O., D. A. L. Lourenco, S. Tsuruta, Y. Masuda, I. Aguilar, A. Legarra, T. J. Lawlor, and I. Misztal. 2015. Hot topic: Use of genomic recursions in single-step genomic best linear unbiased predictor (BLUP) with a large number of genotypes. J. Dairy Sci. 98:4090-4094.
- ↑ Masuda Y., I. Misztal, S. Tsuruta, A. Legarra, I. Aguilar, D.A.L. Lourenco, B.O. Fragomeni, T.J Lawlor. 2016. Implementation of genomic recursions in single-step genomic best linear unbiased predictor for US Holsteins with a large number of genotyped animals. J. Dairy Sci. 99:1968-74.
- ↑ Tsuruta, S., D. Lourenco, Y. Masuda, D.W. Moser, and I. Misztal. 2016. Practical approximation of accuracy in genomic breeding values for a large number of genotyped animals. J. Anim. Sci. 94:162.
- ↑ Edel, C., E.C.G. Pimentel, M. Erbe, R. Emmerling, and K.U. Gotz. 2019. Short Communication: Calculating analytical reliabilities for single-step predictions. J. Dairy Sci. 102:1-7.
- ↑ Misztal, I. and Wiggans, G.R. 1988. Approximation of prediction error variance in large-scale animal models. J. Dairy Sci. 71: 27-32.
- ↑ Wang, H., I. Misztal, I. Aguilar, A. Legarra, and W. M. Muir. 2012. Genome-wide association mapping including phenotypes from relatives without genotypes. Genet. Res. 94(2):73-83.
Single-step Hybrid Marker Effects Models (Suggested writer: Bruce Golden)
Interim Calculations
Bias
(in)complete reporting / contemporary groups / preferential treatment (Suggested writer: Bob Weaber
Accuracy (Suggested writer: Matt Spangler)
meaning of accuracy
what impacts accuracy
different definitions of accuracy (true, BIF, reliability)
Variance components (Suggested writer: Steve Kachman)
Impact on EPD, accuracy, genetic gain (Suggested writer: Steve Kachman)
Heterogeneous variance
Connectivity (Suggested writer: Ron Lewis)
Measures of (Suggested writer: Ron Lewis)
==Impact on GE== (Suggested Writer: Ron Lewis)